Time to read: 6 min

Fluid mechanics is one of the four branches of mechanics, the study of how fluids behave at rest or in motion — and you’re likely to use this knowledge as an engineer in real practice fairly often. I have used fluid mechanics to design heat exchangers for airplanes, to predict the flow of chemical solutions in a plating tank, determine the best method to dry parts after cleaning them, and to describe the impact that vortex generators have on fuel efficiency of an airplane. 

While you may not use fluid mechanics in your career as much as I have, it’s still a critical area to understand — it helps to explain phenomena in the world around us, including aerodynamics, propulsion, combustion, particle physics, meteorology, and astronomy.

Basis of Fluid Mechanics

Fluid mechanics encapsulates multiple pairs of concepts — first, statics and dynamics, then compressible and incompressible, then real and ideal flow types. And real flow is further divided into laminar and turbulent flow. 

Basis of Fluid Mechanics

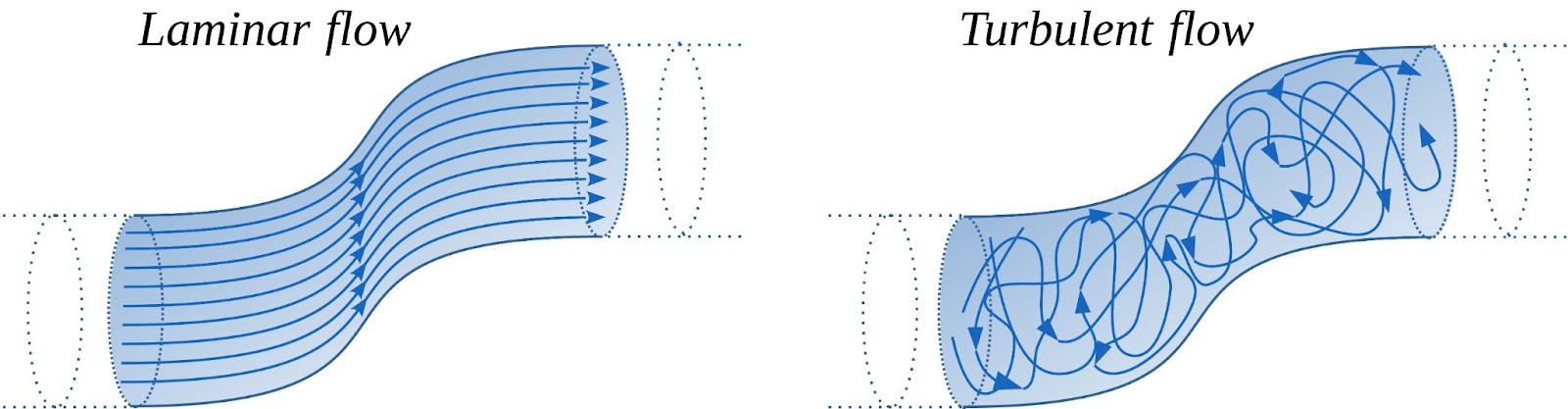
The basis for fluid mechanics is based upon the interplay of five physics principles: 

  1. Second law of thermodynamics: limits the processes that can occur according to the first law of thermodynamics (law of conservation of energy) because energy also has a quality and not just a quantity to be preserved. Specifically, this law states that any naturally occurring process will always cause the universe’s entropy to increase; or the total entropy of an isolated system will not reduce over time. This law also provides a direction for heat transfer that always occurs from a hot body to a cold body (that’s why the HVAC system in your home adds heat in the winter and removes it in the summer — it doesn’t generate cold).
  2. Conservation of mass: in a chemical reaction, mass is neither created nor destroyed.
  3. Conservation of linear momentum: linear momentum is constant before and after a collision of two colliding objects (remember: linear momentum is equal to the mass of an object times the velocity of the object).
  4. Conservation of angular momentum: angular momentum is constant for a system with no external torque (remember: angular momentum is equal to the radius of rotation times the linear momentum).
  5. Conservation of energy: energy is neither created nor destroyed, it simply changes forms (think of a swinging pendulum).

These five principles are best understood when studying fluid dynamics, which is the study of how fluids move and interact with each other. It’s based on the principles of conservation of mass and energy, which states that the total mass and energy of an isolated system must remain constant. 

And the application of principle five to frictionless, laminar flow results in a relationship amongst pressure, velocity, and density which is known as Bernoulli’s Law — this law is defined by Bernoulli’s Equation or the Bernoulli Equation (sometimes referred to as the Bernoulli Principle or Bernoulli’s Principle). 

Origin of Bernoulli’s Equation

Origin of Bernoulli’s Equation

Daniel Bernoulli was a famous Swiss mathematician in the late 18th century, and he impacted many areas of scientific importance including atomic theory, the theory of risk, thermodynamics, and his most relevant work for our purposes, hydrodynamics, which was published in his book Hydrodynamica in 1738.

There are a few important relationships to understand about frictionless laminar flow before diving into Bernoulli’s Equation:

  1. As the speed of a fluid increases, the pressure decreases (same is true in reverse)
  2. Mass and energy are conserved
  3. The sum of pressure and kinetic plus pressure and potential energy densities is constant over time and over a streamline

Bernoulli’s Equation is rooted in common fluid mechanics concepts, especially conservation of energy. Read on for the derivation of Bernoulli’s Equation. 

Bernoulli’s Equation Explained

The core of Bernoulli’s Equation is the conservation of energy — which states that for a closed system, the total energy of the system must remain constant. For a moving fluid, the energy of the system can be broken down into two components which are measures of the amount of energy of the system at any given point: pressure and velocity. 

Let’s review the derivation of Bernoulli’s Equation to get a better understanding of its components and potential applications. For example, let’s consider an incompressible fluid (like water), moving through a frictionless, converging pipe, as shown below: 

example scenario used to derive Bernoulli’s Equation

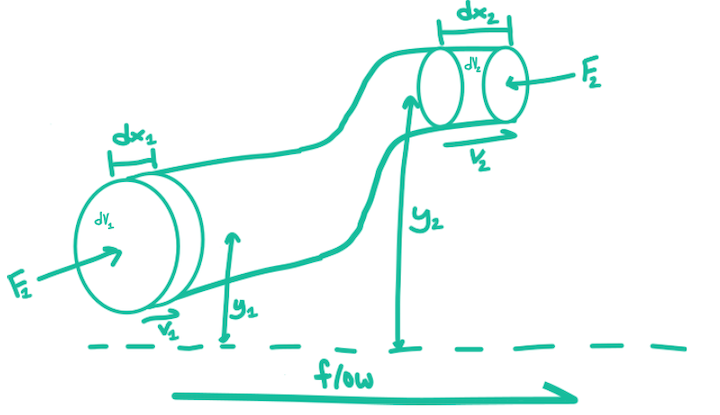
Consider the following assumptions for Bernoulli’s Equation: 

  1. Fluid flow is one-dimensional and steady
  2. Fluid is inviscid (ideal fluid, all surface forces exerted on the boundaries of each small element of the fluid act normal to these boundaries); meaning there are no viscous forces in the fluid
  3. So, there is transfer of energy from kinetic to thermal energy within the fluid
  4. The flow is frictionless
  5. The stress tensor within the fluid is reduced to the pressure of the fluid and is a point function, scalar
  6. The fluid is homogenous
  7. There is no shear stress to account for

For the above scenario, we can define the following variables: 

  • F = force on the fluid to move it a certain distance
  • v = velocity of fluid
  • dx = defines the boundary layer for location 1 and 2 (gives distance ‘x’)
  • V = control volume represented by dV
  • y = height from ground

We can also define these variables for this scenario:

  • P = pressure 
  • = density
  • A = cross-sectional area of pipe
  • m = mass
  • K = kinetic energy
  • U = potential energy
  • g = force due to gravity (universal gravitational constant)

We know that the force at point one and point two are equal to the pressure of the fluid times the cross-sectional area of the pipe at that location: 

F=AP

F1 = A1P1

F2 = A2B2

Knowing that work is force times distance, we can calculate the change in work from point 1 to point 2 as: 

dW = F1dx1 – F2dx2

dW = P1A1dx1 – P2A2dx2

Knowing that volume is equal to cross-sectional area(A) times width (dx) gives:

dW = P1dV1 – P2dV2

dW = (P1 – P2) dV

Work on the fluid is a result of moving the fluid against the force of gravity and changing kinetic energy of the fluid. This change in kinetic energy can be expressed as:

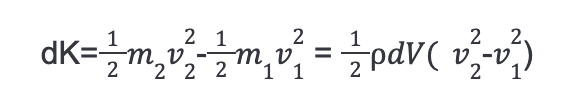
The change in potential energy from location one to location two can be expressed as:

dU=m2gy2 – m1gy1 = pdVg(y2-y1)

Now, knowing that the work done is equivalent to the kinetic and potential energies, due to the Law of Conservation of Energy, we get the following relationship: 

dW=dK+dU

Substituting the above equations for W, K and U gives:

equations W, K and U

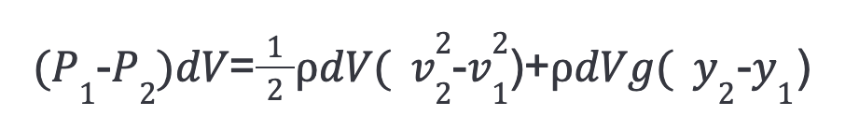
Dividing all the equation by dV gives:

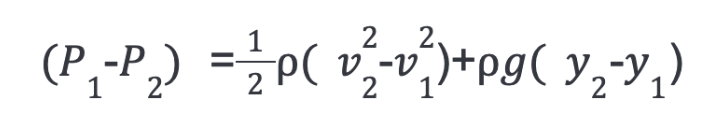
Rearranging the equation so that all the location 1 variables are on the left and location 2 variables are on the right gives Bernoulli’s Equation:

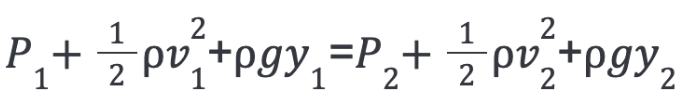
From this last equation, we can see that the total mechanical change energy of any part of the fluid is a result of the work (potential and kinetic energy changes) done by the fluid external to the part, and is also a result of the changes in pressure from one location to another. Simplifying this for any point along the streamlined flow gives the more recognizeable form of Bernoulli’s Equation: 

P   –  
1
2
pv2 + pgy   =   constant

This constant is sometimes known as the Bernoulli Equation Constant, which means that the sum of the terms on the left-hand remains constant, regardless of what location along the flow’s path you choose. 

Bernoulli’s Equation in Real Life

If you are a mechanical engineer, biomedical engineer, aerospace engineer, or any type of engineer that deals with fluids, you will use Bernoulli’s Equation in real world applications. For example, in aeronautical engineering, Bernoulli’s Equation explains the flow of fluid over an aircraft and how an aircraft stays in the air. In simple terms, airplanes fly because air flows over the curved surfaces of the wings, which creates a low pressure area that accelerates the air traveling over the top of the wing and creates lift. 

example of Bernoulli’s Equation application

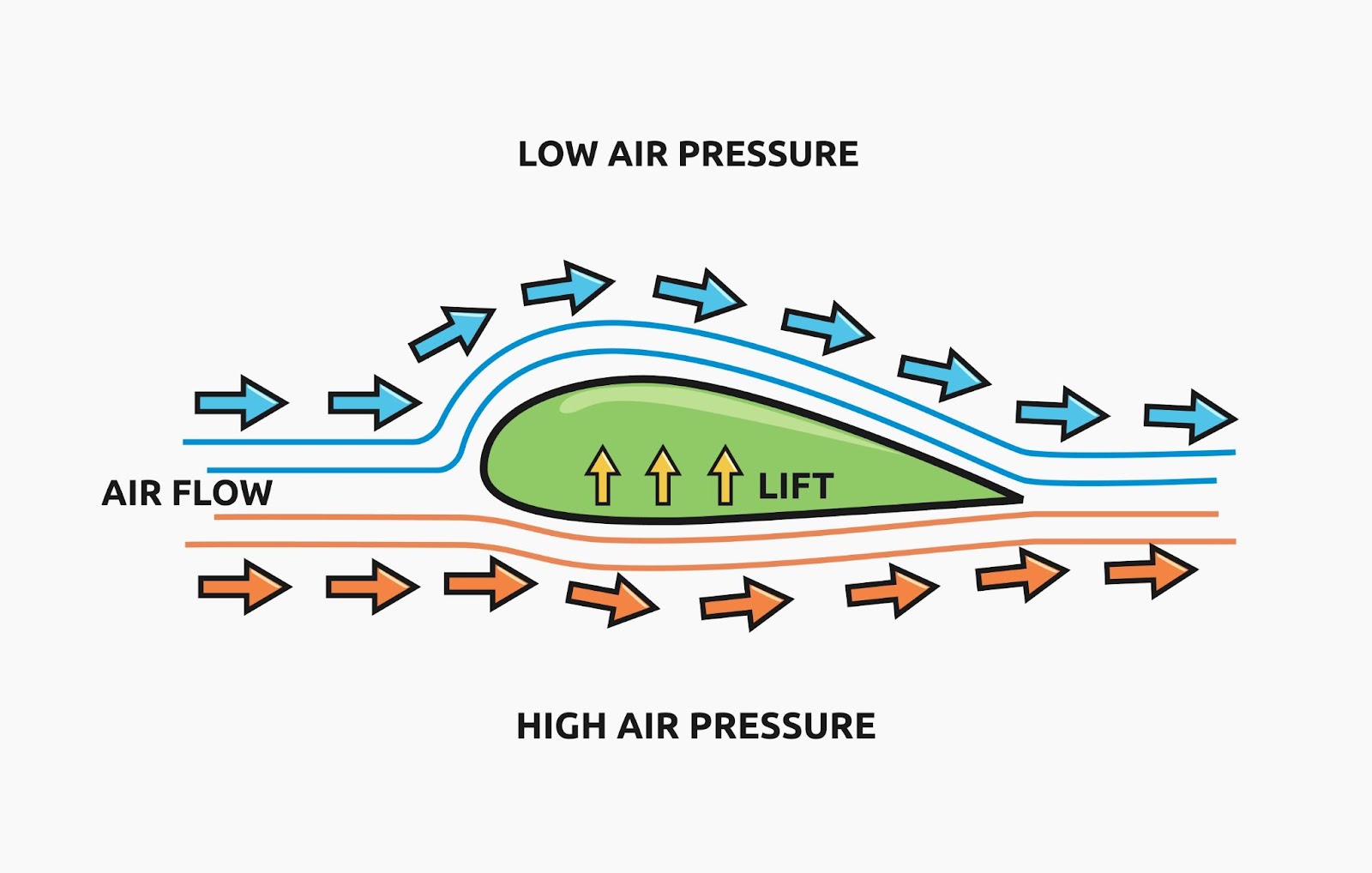
In biomedical engineering, Bernoulli’s Law explains the flow of blood through veins and arteries in the cardiovascular system. Other common applications of Bernouilli’s Law include: 

  • flow through nozzles and channels
  • drag force in watercraft and automobiles
  • fluid flow measuring devices

Bernoulli’s Law is a fundamental principle of fluid dynamics that describes the relationship between the pressure, velocity, and density of a moving fluid. It has a wide range of applications in many different fields, ranging from aeronautical engineering to medicine. That’s why understanding Bernoulli’s Law is essential for anyone who wants to work with fluids.

Fictiv: Complex Parts at Ridiculous Speeds

Comprehensive understanding of Bernoulli’s Equation is key to crafting good designs  for parts involved with flowing fluids, but to get good parts, you also need a top-notch production parter. Fictiv is that partner who manufactures the quality, complex parts you need at ridiculous speeds. 

Fictiv is your operating system for custom manufacturing that makes part procurement faster, easier, and more efficient. In other words, Fictiv lets engineers, like you, engineer. Create an account and upload your part to see what our instant online CNC quote process, design for manufacturability feedback, and intelligent platform can do for you.