Time to read: 4 min
As a design engineer, you should be intimately familiar with the essential mechanical properties that quantify how materials respond to load or stress application — and Poisson’s Proportion and Young’s Modulus are two of those properties. These properties offer critical information for engineers looking to achieve robust designs that can withstand demanding environments.
This article discusses the implications, importance, applications, and the exchange between Poisson’s Proportion and Young’s Modulus. Whether you’re a seasoned designer looking for a refresher or a new engineer trying to get a handle on the essential mechanics of materials, we have what you’re looking for.
Young’s Modulus (E)
Young’s Modulus is also known as the elastic modulus of a material (note: there are three types of elastic moduli). It is signified as E, and gauges a material’s elasticity or ability to withstand deformation under applied stress by measuring how much a material stretches or compresses when exposed to an external force.
Young’s Modulus is determined utilizing the pressure-strain relationship, where stress (𝛔) is the applied power per unit region, and strain (𝜀) is the subsequent deformation ratio.
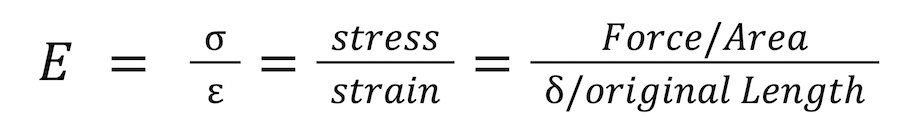
Exploring Young’s Modulus
Young’s Modulus evaluates the connection between stress and strain of a material. Numerically, it is characterized as the proportion of pressure (force applied per unit region) to strain (change long per unique length) along the versatile area of the material’s pressure strain bend.
Young’s Modulus mirrors a material’s capacity to oppose deformity under load, and is communicated in units of tension (Pascals or N/m²). Materials with high Young’s Modulus values are stiffer and require more energy to incite twisting, while those with lower values are more adaptable.
Poisson’s Ratio (𝛎)
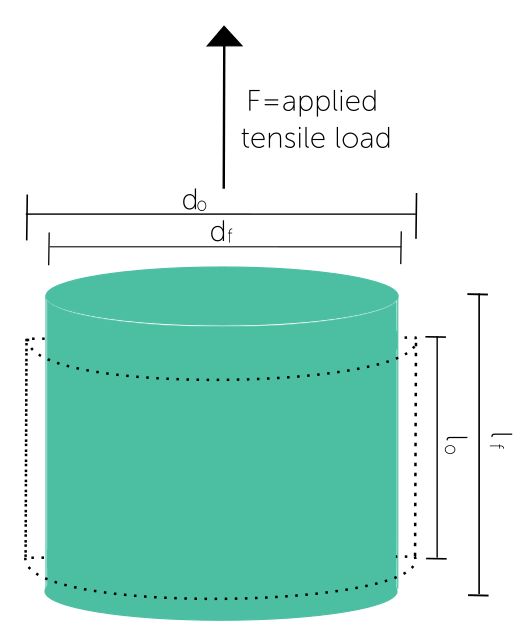

Poisson’s Proportion, or Poisson’s Ratio, known as ν, is a numerical representation of the parallel compression of a material when exposed to an applied load. It is the ratio of the lateral strain (sidelong compression) to the linear strain (prolongation). Poisson’s Ratio explains how a material’s volume changes when subjected to applied stress.
Understanding Poisson’s Ratio:
In easier terms, Poisson’s Ratio evaluates how a material changes in width when it is extended or compacted along its length. The proportion is determined by dividing the cross-over strain (change in width) by the hub strain (change long). For most materials, Poisson’s Proportion commonly falls inside the scope of 0.0 to 0.5, with elastic materials displaying values near 0.5 because of their high compressibility and materials like steel having lower values around 0.3 because of their solidness.
Material Behavior and Applications

Materials with high Young’s Modulus are firm and resist distortion and require a higher load for a resulting strain to occur, making them reasonable for load-bearing applications. Here are some examples of materials with high modulus of elasticity¹:
- Diamond has the highest elastic modulus of any known material due to its high valence electron density (1220 GPa)
- Tungsten carbide for similar reasons as diamond (450-650 GPa)
¹At standard room temperatures, unless otherwise noted; values for educational purposes only. Always consult material data sheets for specific properties for your material
- Sapphire (435 GPa)
- Beryllium (287 GPa)
- Chromium-Molbydenum Steels like 4140 (213 GPa)
- 316 Stainless steel (195 GPa)
Low Young’s Modulus materials are adaptable and are utilized where deformity is beneficial — like gaskets and o-rings. An example of a material with a low modulus of elasticity is silly putty. Poisson’s Proportion influences the way the material behaves during pressure or extending. Materials with low Poisson’s Proportion contract less along the side, prompting clasping.

Stress-Strain Correlation
Young’s Modulus impacts the slant of the pressure strain bend on a stress vs. strain curve, and is the slope of the stress-strain curve for a material under compressive or tensile loading. Higher E values mean that the slope of the curve is less steep, and the material has more prominent firmness. Poisson’s Ratio influences the connection among pivotal and parallel strains, with low qualities demonstrating insignificant sidelong constriction.
Contrasting Poisson’s Proportion and Young’s Modulus
Poisson’s Proportion is a dimensionless amount, while Young’s Modulus has units of tension. Poisson’s Proportion portrays volumetric changes, while Young’s Modulus describes pivotal deformation.
Estimation and Testing:

Young’s Modulus is estimated utilizing physical testing strategies like pressure, pressure, and twisting tests. Poisson’s is not entirely settled by checking horizontal and pivotal strain during distortion tests.
Material Determination and Plan:
Engineers consider Young’s Modulus while choosing materials for explicit applications. High E materials give high rigidity and hold energy, while low E materials assimilate energy. Poisson’s Proportion influences your configuration where clasping or mishappening should be controlled.
Pro-Tip: To learn more about designing with the best Young’s Modulus and Poisson’s Ratio values, check out How to Design for Stiffness Using Material Properties.
The Interplay and Applications
Poisson’s Proportion and Young’s Modulus have a complex association through a material’s reaction to mechanical pressure.
When exposed to ductile or compressive forces, a material with a higher Poisson’s Proportion will often extend horizontally and contract pivotally. This parallel development counters the prolongation or pressure, and influences how the material generally deforms. Young’s Modulus impacts how much a material misshapes under the applied pressure.
Together, these properties impact how materials behave in structures, deciding elements like burden circulation, steadiness, and diversion.
Understanding the differences between Poisson’s Proportion vs Young’s Modulus is critical for planning and breaking down structures that can endure forces in the real world. While Poisson’s Proportion portrays a material’s propensity to change in width when extended or packed, Young’s Modulus characterizes its solidness and capacity to oppose disfigurement.
These properties establish the groundwork for anticipating and understanding how materials act under different mechanical stresses. As engineers and materials scientists keep pushing the limits of development and effectiveness, a strong perception of Poisson’s Proportion and Young’s Modulus stays a foundation of fruitful material determination, plan improvement, and underlying respectability.
For materials stiff or strong, flexible or resistant to deformation, Fictiv is your ultimate CNC machining partner. The accessibility, convenience, cost efficiency, fast turnaround times, quality assurance, customization options, enhanced communication, and scalability Fictiv provides is unparalleled in the precision machining industry.

Choose Fictiv for all your CNC part manufacturing needs. Sign up for a free account and see how beneficial our CNC machining services can be for you!








